四种常见滤波和 MATLAB 仿真:一阶 RC 低通滤波,二阶 IIR 低通滤波,五阶 FIR 低通滤波,卡尔曼滤波
一阶 RC 低通滤波
FilterData = cof * RawData + (1.000f - cof) * FilterData;
一阶 RC 低通滤波又叫一阶惯性滤波,因为本质上也是积分滤波器。
不能滤除频率高于采样频率的二分之一的干扰。
cof是一阶RC低通滤波参数,代表新采样值在滤波结果中的权重。
滤波系数越小,滤波结果越平稳,灵敏度越低。
滤波系数可以理解为对采样值的相信程度。
float Cof = = 1.0 / (1.0 + (1.0 / 2Pi * T(s) * fc));
上面是cof的计算公式。但一阶 RC 低通滤波在实际情况也可以不按照公式计算的结果,用上位机比较原始值和滤波后数值波形来试凑出来一版系数也是可行的。
二阶 IIR 低通滤波
IIR 滤波公式:
\[y_n=\frac{1}{b_0}\left(\sum_{k=0}^{n}{b_kx\left(n-k\right)}-\sum_{k=1}^{n}{a_kx\left(n-k\right)}\right)\]或是
\[y_{\left(n\right)}=b_0x_{\left(n\right)}+b_1x_{\left(n-1\right)}+\ldots+b_Mx_{\left(n-M\right)}-a_1y_{\left(n-1\right)}-\ldots-a_Ny_{\left(n-N\right)}\]IIR滤波就是这个个方程。yn为输出数据,xn为输入数据,a和b为滤波器的系数。
C语言实现:
#define ORDER 2
typedef struct {
float A[ORDER + 1];
float B[ORDER + 1];
float OriginData[ORDER + 1];
float FilterData[ORDER + 1];
} LpfIIR2nd_t;
/**
* @brief 二阶IIR低通滤波器
* @param[out] lpf : 滤波结构数据指针
* @param[in] rawData : 原始数据
*/
void LowPassFilterIIR2nd(LpfIIR2nd_t* lpf, float rawData)
{
uint8_t i = 0;
// 递推旧值
for (i = ORDER; i > 0; i--) {
lpf->OriginData[i] = lpf->OriginData[i - 1];
lpf->FilterData[i] = lpf->FilterData[i - 1];
}
// 计算滤波结果
lpf->OriginData[0] = rawData;
lpf->FilterData[0] = lpf->B[0] * lpf->OriginData[0]; // NUM 分子
for (i = 1; i <= ORDER; i++) {
lpf->FilterData[0] = lpf->FilterData[0] + lpf->B[i] * lpf->OriginData[i] - lpf->A[i] * lpf->FilterData[i];
}
}
最后计算滤波结果也可以写成
lpf->FilterData[0] = (lpf->B[0] * lpf->OriginData[0] + lpf->B[1] * lpf->OriginData[1] + lpf->B[2] * lpf->OriginData[2] - lpf->A[1] * lpf->FilterData[1] - lpf->A[2] * lpf->FilterData[2]) / lpf->A[0];
注意在使用滤波前要先初始化结构体的滤波系数。只需要初始化一次即可。
其中分子系数是成对出现的,可以先合并来提高运算效率。
也可以优化成int型或是用移位器和加法器来代替乘法。
滤波系数的计算:
/**
* @brief 二阶 IIR 低通滤波
* APM 和 PX4 内的计算系数方式
*/
void AccLowpassIIR2Filter_E(void)
{
const float sample_freq = 500;
const float _cutoff_freq = 200;
const float fr = sample_freq / _cutoff_freq;
const float ohm = tanf(M_PI_F / fr);
const float c = 1.0f + 2.0f * cosf(M_PI_F / 4.0f) * ohm + ohm * ohm;
const float _b0 = ohm * ohm / c;
const float _b1 = 2.0f * _b0;
const float _b2 = _b0;
const float _a1 = 2.0f * (ohm * ohm - 1.0f) / c;
const float _a2 = (1.0f - 2.0f * cosf(M_PI_F / 4.0f) * ohm +ohm * ohm) / c;
// lFilter[0] = Origin[0] * _b0 + Origin[1] * _b1 + Origin[2] * _b2 - Filter[1] * _a1 - Filter[2] * _a2;
}
滤波系数的计算也可以使用MATLAB仿真的方式计算:
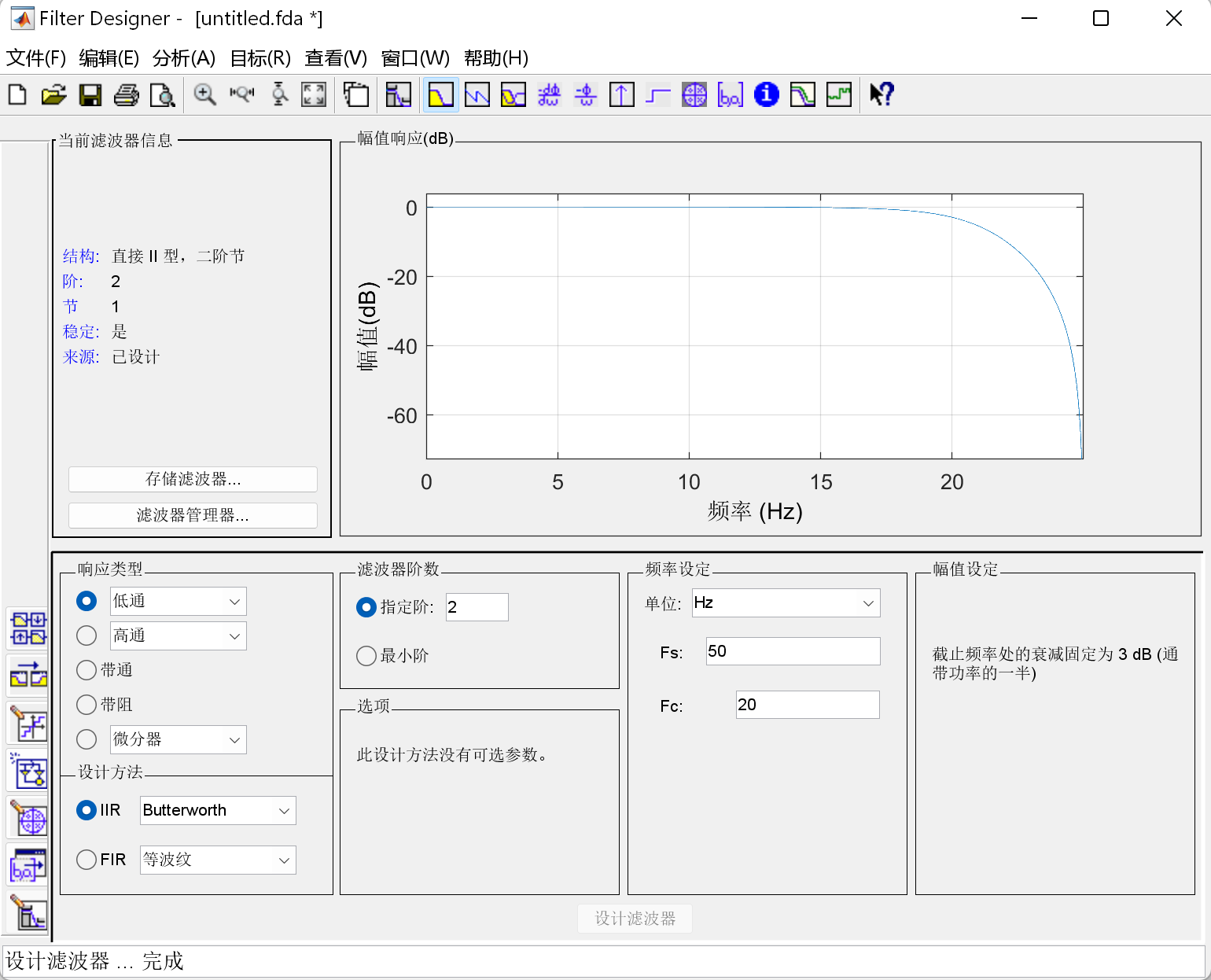
打开 Matlab 在APP中选择 Filter Designer(fdatool)
-
设计方法(Design Method)用于选择IIR滤波器还是FIR滤波器。这里我们选择IIR滤波器,类型选择Butterworth。当然也可以选择其他类型,不同类型的频率响应不同,选择后默认的滤波器结构是直接II型。
-
响应类型(Response Type)用于选择低通、高通、带通、带阻等类型。这里选择选择低通(Lowpass)。
-
频率设定(Frequency Specifications)用于设置采样频率以及截止频率,这里填入500以及50,即采样率为500Hz,50Hz以上的频率将被滤除掉。
- 滤波器阶数(Fiter Order )选择指定滤波器阶数为二阶。
- 参数设置好后点击设计滤波器(Design filter)按钮,将按要求设计滤波器。
- 默认生成的IIR滤波器类型是直接Ⅱ型,每个Section是一个二阶滤波器(Direct-Form II, Second-Order Sections)。
- 在工具栏上点击右数第五个滤波器系数(Filter Coefficients)图标,或菜单栏上选择分析(Analysis)→滤波器系数(Filter Coefficients),即可查看生成的滤波器系数。
- 最后在菜单栏点击编辑(edit)→转换为二节点(Convert to Single Section),即是我们最终用的滤波器系数。在MATLAB里,IIR公式中的ab又分别叫做分子(Numerator)和分母(Denominator)。
- 左边实现模型(Realize Model)还可以生成Simulink模型进行仿真。
五阶 FIR 低通滤波
FIR 滤波公式:
\[y_{(n)}=\sum_{k=0}^{N-1}{k_{(k)}x_{(n-k)}}\]FIR滤波就是这个个方程。x(n)为输入信号,k(n)为FIR滤波系数,y(n)为经过滤波后的信号;N表示FIR滤波器的抽头数,滤波器阶数为N-1。
C语言实现:
#define ORDER 5
void FIR5Filter(void)
{
const float H[ORDER + 1] = {...};
Filter[0] = 0;
for (uint16_t j = 0; j < ORDER + 1; j++) {
Filter[0] += H[j] * Origin[j];
}
}
滤波系数的计算:
-
FIR滤波器设计方法有多种,如图4所示,最常用的是窗函数设计法(Window)、等波纹设计法(Equiripple)和最小二乘法 (Least-Squares)等。
- 设置频率响应的参数,包括采样频率Fs、通带频率Fpass和阻带频率Fstop
- 可以使用ARM官方DSP库实现FIR和IIR滤波,提高运行速度和效率。
卡尔曼滤波
算法的思想是,根据当前的仪器”测量值” 和上一刻的 “预测量” 和 “误差”,计算得到当前的最优量,再预测下一刻的量。卡尔曼滤波器就是一个带有预测功能的低通滤波器。
一维卡尔曼滤波C语言实现:
typedef struct {
float x; // state
float A; // x(n)=A*x(n-1)+u(n),u(n)~N(0,q)
float H; // z(n)=H*x(n)+w(n),w(n)~N(0,r)
float q; // process(predict) noise convariance
float r; // measure noise(error) convariance
float p; // estimated error convariance
float gain; // kalman gain
} kalman1_filter_t;
/**
* @brief 一阶卡尔曼滤波初始化
* @param[out] state : 滤波结构数据指针
* @param[in] q & r
*/
void kalman1_init(kalman1_filter_t *state, float q, float r)
{
state->x = 0.0f;
state->p = 0.0f;
state->A = 1.0f;
state->H = 1.0f;
state->q = q;
state->r = r;
}
/**
* @brief 一阶卡尔曼滤波
* @param[out] state : 滤波结构数据指针
* @param[in] z_measure : 原始数据
*/
float kalman1_filter(kalman1_filter_t *state, float z_measure)
{
/* Predict */
// 时间更新(预测): X(k|k-1) = A(k,k-1)*X(k-1|k-1) + B(k)*u(k)
state->x = state->A * state->x;
// 更新先验协方差: P(k|k-1) = A(k,k-1)*A(k,k-1)^T*P(k-1|k-1)+Q(k)
state->p = state->A * state->A * state->p + state->q;
/* Measurement */
// 计算卡尔曼增益: K(k) = P(k|k-1)*H(k)^T/(P(k|k-1)*H(k)*H(k)^T + R(k))
state->gain = state->p * state->H / (state->p * state->H * state->H + state->r);
// 测量更新(校正): X(k|k) = X(k|k-1)+K(k)*(Z(k)-H(k)*X(k|k-1))
state->x = state->x + state->gain * (z_measure - state->H * state->x);
// 更新后验协方差: P(k|k) =(I-K(k)*H(k))*P(k|k-1)
state->p = (1 - state->gain * state->H) * state->p;
return state->x;
}
-
一维卡尔曼滤波全部是标量计算
-
R固定,Q越大,代表越信任侧量值,Q无穷代表只用测量值(Q/R取0无意义)Q/R决定了滤波器的稳态频率响
应。Q增大和R减小都会导致卡尔曼增益K变大
-
测量噪声大 R需要设置的较大
-
模型不准确 Q需要增大
-
卡尔曼增益的值越大,意味着越相信测量值的输出,从而使得估计值倾向于测量值,收敛速度越快,最优估计值震荡越明显
-
A B H 根据模型来确定
-
P变大也会导致卡尔曼增益变大,但是很快会迭代至稳定值,因此P的初始值只会对前几个周期的估计值有影响。
-
二维及以上的卡尔曼滤波运算过程涉及到大量的矩阵运算,如果将矩阵运算拆开成基本的四则运算扩展性很差,并且在遇到例如求逆运算的时候比较麻烦。可以使用ARM的DSP库里面的矩阵运算功能