元素的处理方案：环岛，坡道，三叉，以及直道和弯道的速度控制方案

元素处理分到了两篇文章中：本篇元素的处理方案以及全向组麦轮的特色控制方案。

环岛：

• 我们对于环岛的识别使用的是稳定的电磁判断方案。内侧两个横向电感会在环岛切点处达到极值，以此来判断环岛。

• 入环时使用摄像头补线，并开始计算陀螺仪z轴积分。陀螺仪大于60度入环补线结束，陀螺仪大于200度开始摄像头识别出环，若出环判断失败陀螺仪大于250度强制开始出环，陀螺仪大于355度出环完成。

• 当陀螺仪大于100度小于225度时，累加环内转向环PID输出量，记录环内转角输出，目的是用环内计算环岛内平均打角。当出环预备标志位置1后，将计算值强制赋给转向环输出，实现出环使用稳定的环内姿态。出环不仅可以使用环内状态也可使用入环状态，我们测试发现使用环内姿态更为稳定。

• 电感判断环岛的问题在于出环后会重复判断，所以需要写一个出环后短时间0.8s内不再识别第二个环岛。

• 另外判断小环岛和大环岛 可以记录车身0-60度时间或是编码器脉冲数。

• 对于环内巡线，由于我们是30cm摄像头限高，所以使用正常巡线也能有不错的效果。但使用正常的摄像头中值会偏向一侧，可以在左右环岛分别赋予不同的摄像头中值。

• 环内属于稳定而又简单的元素，入环并判断车身稳定后可以环内加速。如果使用记录环内姿态用于出环，则出环速度需要与环内速度相同，相当于在环岛元素内只在入环减速其他时刻都在加速。

坡道：

• 我们使用 TFMiniPlus 激光雷达测距来判断坡道。当距离降到一定阈值下即可判断坡道。
• 我们将 TFMiniPlus 竖直倾斜安装，此时测距点在赛道上。水平安装同样可以，不过水平安装测距点不稳定，赛道铺设场地有限的情况下可能会与赛道挡板误判。
• 在识别到坡道后开始计步（Vy轴向编码器数值累加），路程判断在上坡进行到三分之一稳定后时开启加速并在下坡时关闭加速。路程经过上坡三分之一后对Vx和w两个自由度的每次输出进行限幅防止过量打角抖动，上坡前三分之一不限幅是为了让车身修正姿态。
• 判断坡道结束可以仅使用计步，当距离超过测定阈值后结束坡道。也可以当测距再次出现极小值时判断坡道结束。为了防止下坡时二次识别，可以加上下坡后0.5s内不再识别第二个坡道。另外还可以用走过一定距离后识别正常赛道结束坡道，判断条件为计步超过小阈值并且测距恢复为正常距离值一定次数后即可判断结束。

三岔：

• 我们的控制方案三岔路口的一条路分为八步处理。

  第零步是预判断三岔，预判断后将加速降为加速计算量的一半。毕竟要给三斤多的麦轮车留够减速的时间

  当完全判断为三岔时，因为摄像头判断区域与车身实际位置存在距离，且在摄像头高度和角度不变的情况下，距离也不会变。所以第一步为前进一定距离至三岔中心点，同时开始90度旋转舵机。

  第二步在前进完成后使车身旋转30度与入口赛道平行。这样可以防止仅摄像头补线输出值过大，进入三岔出现抖动的问题。

  因为舵机旋转需要时间，且旋转完成后摄像头处理速度较慢，旋转完成时的摄像头输出值不稳定，旋转后不能立刻切为摄像头循迹。所以第三步为车身横向平移一定距离等待摄像头稳定。

  第四步即为三岔内横向循迹。我们出现的情况是右三岔循迹良好左三岔严重偏向外侧，所以右三岔基础速度和加速最大值都会大于左三岔。另外对于三岔内偏向一侧也可以使用与环岛相同的处理办法，即左右分别赋予不同的摄像头中值。

  第五步在预判断出三叉后开启转角输出限幅，限幅至仅能小幅度修正姿态，防止补线补到三岔的另一侧致使出三岔内切。并且也将加速降为加速计算量的一半。

  第六步在判断到出三岔后前进一定距离至中心点，同时开始转正舵机，原因同第一步。

  第七步在前进完成后使车身旋转150度。

  第八步在旋转后前进一定距离，原因同第三步。至此三叉的一条边处理结束。左三叉也是相同的处理流程。

直道加速：

​全向组在赛道上匀速循迹很大可能不会有一个较高的速度，所以直道加速就显得很有必要。我们使用了五种直道加速的判断条件。

中线判断加速：

判断图像上半部分中线与赛道两边界无交点即可加速。

for (i = startRow; i < endRow; i++) {
    if ((endRow - startRow) < 5) {
        break;
    }   //行数过少取消判断

    if (middleStandard - leftBlack[i] > 4 && rightBlack[i] - middleStandard > 4) {
        rowCount2++;
    } else if (middleStandard - leftBlack[i] > 2 && rightBlack[i] - middleStandard > 2) {
        rowCount++;
    } else {
        break;
    }

    if (rowCount == endRow - startRow) {
        Gear = 8;
    }
    if (rowCount2 == endRow - startRow) {
        Gear = 10;
    }
}   //判断中线上半部与赛道两边界无焦点即可加速

顶部有效图像判断加速：

在正常计算中线误差的 for 循环内 当计算完前三分之一使用面积时，计算有效图像前三分之一的误差，用于远处判断加速。这样可以使运算更为高效。

顶行采样判断直道加速：

分别计算speed_line为20, 25, 30这三行的误差，并取最大值用于判断加速。

speedLineErr = (ABS)((  5 * middleLine[speedLine] +
                        2 * middleLine[speedLine + 1] +
                        3 * middleLine[speedLine - 1]) / (10) - middleStandard);

有效行判断加速：

当有效行在顶部时，给予加速。可以简单使用分段打表的方式，也可以拟合成线性关系。记得写限幅！

距离判断加速：

实际走过一定距离的直道, 就算是直道。有些时候小s不会判断加速，这时只是用车身姿态来判断，可以解决这些正常判断较为难以处理的情况。注意这样加有滞后性, 加速量不要给多。

if (ABS((int16)(fabsf(carSpeedA))) < speedZone) {
    disAccCount ++;
} else {
    disAccCount = 0;
}

if (disAccCount >= 500)    disAccCount = 500;    //限幅

if (disAccCount > countZone) {
    Gear = 3;
}

弯道控制：

弯道的速度的公式 $f = \mu\ mg = m\ \frac{v^2}{R}$ 。F是摩擦力；$\mu$是摩擦系数，由地面和轮胎决定；R是转弯半径。由于地面和轮胎在过弯时是给定的，这样在比赛中我们为了保证V大，只能保证更大的转弯半径。R越大，速度V就越大。所以稳定沿着电磁线循迹并不一定是最优解，最好是采用外内外切弯。即入弯时贴弯道的内弯，出弯时贴外弯。这种情况下赛车通过整个弯道过程中行车线半径是固定的，即定曲率行车线。弯道的速度控制方案也最好为，入弯减速避免打滑，出弯加速节约时间。

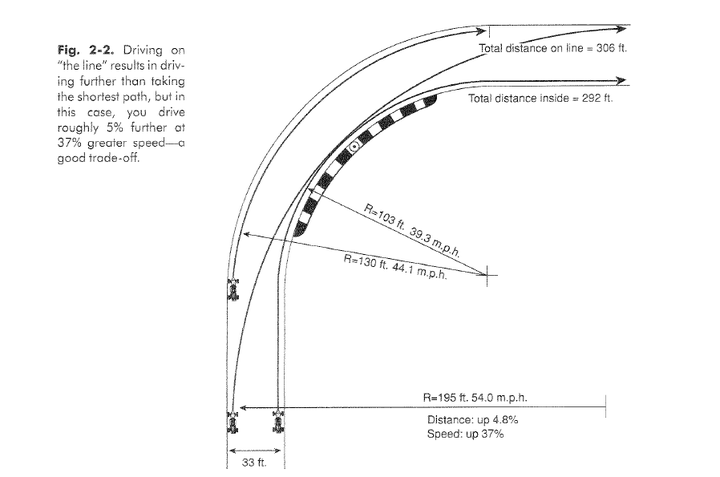
实践中发现通过调整纯跟踪算法的预瞄距离就能够有这样的效果，可以有效提高路径规划的最优性。

元素处理分到了两篇文章中：本篇元素的处理方案以及全向组麦轮的特色控制方案。